ECDHE密钥协商,ECDHE算法实现要复杂很多,主要分为两部分:diffie-hellman 算法(简称为 DH)及 ECC(椭圆曲线算术),他们的安全性都是建立在离散对数计算很困难的基础上。
概述DH算法原理
DH(diffie-hellman,赫尔曼)密钥交换协议/算法使用了数学原理,但是很容易理解。DH由Whitfield Diffie和Martin Hellman在1976年公布的一种密钥一致性算法。DH是一种建立密钥的方法,而不是加密方法。然而,它所产生的密钥可用于加密、进一步的密钥管理或任何其它的加密方式。DH密钥交换算法及其优化首次发表的公开密钥算法出现在Diffie和Hellman的论文中,这篇影响深远的论文奠定了公开密钥密码编码学。
先介绍几个基本概念:
素数:素数又称质数,有无限个。一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,换句话说就是该数除了1和它本身以外不再有其他的因数;否则称为合数。
原根:设m是正整数,a是整数,若a模m的阶等于φ(m),则称a为模m的一个原根。(其中φ(m)表示m的欧拉函数)
离散对数:就是在整数中,一种基于同余运算和原根的一种对数运算。
离散对数:如果对于一个整数b和素数p的一个原根a,可以找到一个唯一的指数 i,使得: b =(a的i次方) mod p 其中0≦ i ≦p-1, 那么指数i 称为b的以a为基数的模p的离散对数。
Diffie-Hellman 算法的有效性依赖于计算离散对数的难度,其含义是:当已知大素数p和它的一个原根a后,对给定的 b,要计算 i ,被认为是很困难的,而给定 i 计算b 却相对容易。
DH算法示例,如:
假设Client和Server需要协商密钥,p=2579,则原根a = 2
Client选择随机数 Kc = 123做为自己的私钥,计算Yc = a^Kc mod p = 2^123 mod 2579 = 2400,把Yc作为公钥发送给Server。
Server选择随机数Ks = 293作为私钥,计算Ys = a^Ks mod p = s^293 mod 2579 = 968,把Ys作为公钥发送给Client。
Client计算共享密钥:secrect = Ys^Kc mod(p) = 968^123 mod(2579) = 434
Server计算共享密钥:secrect = Yc^Ks mod(p) =2400^293 mod(2579) = 434
上述公式中的Ys,Yc,P, a都是公开信息,可以被中间者查看,只有Ks,Kc作为私钥没有公开,当私钥较小时,通过穷举攻击能够计算出共享密钥,但是当私钥非常大时,穷举攻击肯定是不可行的。
DH算法有一个比较大的缺陷就是需要提供足够大的私钥来保证安全性,所以比较消耗 CPU 计算资源。ECC椭圆曲线算术能够很好的解决这个问题,224位的密钥长度就能达到RSA2048 位的安全强度。ECC的曲线公式描述的其实不是椭圆,只是跟椭圆曲线周长公式形似才叫椭圆曲线加密算术。
ECC安全性依赖于这样一个事实:
P = kQ, 已知k, Q求出P相对简单,但是已知P和Q求出k却非常困难。
上式看起来非常简单,但有如下约束条件:
Q是一个非常大的质数,p,k,q都是椭圆曲线有限域上的离散点。有限域定义了自己的加法和乘法法则,即使kQ的运算也非常复杂。ECC应用于Diffie-Hellman密钥交换过程如下:定义一个满足椭圆方程的有限域,即挑选 p, a, b满足如下方程:
y^2 mod p = (x^3+ax +b) mod p
挑选基点G = (x, y),G的阶为n。n为满足nG = 0 的最小正整数。
Client选择私钥Kc (0 <Kc<n ),产生公钥Yc =Kc *G
Server选择私钥Ks并产生公钥Ys =Ks*G
Client计算共享密钥K = Kc*Ys,server端计算共享密钥Ks*Yc,这两者的结果是一样的,因为:Kc*Ys = Kc*(Ks*G) = Ks*(Kc*G) = Ks*Yc
由上面描述可知,只要确定p, a, b就能确定一条有限域上的椭圆曲线,由于不是所有的椭圆曲线都能够用于加密,所以p, a, b的选取非常讲究,直接关系曲线的安全性和计算速度。
Openssl实现的,也是FIPS 推荐的256位素数域上的椭圆曲线参数定义如下:
质数 p = 115792089210356248762697446949407573530086143415290314195533631308867097853951
阶 n = 115792089210356248762697446949407573529996955224135760342422259061068512044369
SEED = c49d3608 86e70493 6a6678e1 139d26b7 819f7e90
c = 7efba166 2985be94 03cb055c 75d4f7e0 ce8d84a9 c5114abcaf317768 0104fa0d
椭圆曲线的系数 a = 0
椭圆曲线的系统 b = 5ac635d8 aa3a93e7 b3ebbd55 769886bc 651d06b0 cc53b0f63bce3c3e 27d2604b
基点 G x = 6b17d1f2 e12c4247 f8bce6e5 63a440f2 77037d81 2deb33a0f4a13945 d898c296
基点 G y = 4fe342e2 fe1a7f9b 8ee7eb4a 7c0f9e16 2bce3357 6b315ececbb64068 37bf51f5
握手过程中的 ECDHE 密钥协商,如下图
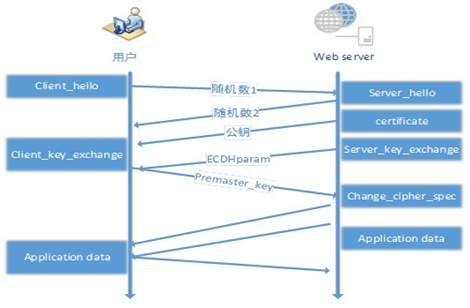
简单介绍了ECC和DH算法的数学原理,我们看下ECDHE在TLS握手过程中的应用。
相比RSA,ECDHE需要多发送一个server_key_exchange的握手消息才能完成密钥协商。
同样以TLS1.2为例,简单描述一下过程:
一、浏览器发送client_hello,包含一个随机数random1,同时需要有2个扩展:
A)Elliptic_curves:客户端支持的曲线类型和有限域参数。现在使用最多的是 256 位的素数域,参数定义如上节所述。
B)Ec_point_formats:支持的曲线点格式,默认都是uncompressed。
二、服务端回复server_hello,包含一个随机数random2及ECC扩展。
A)服务端回复certificate,携带了证书公钥。
B)服务端生成ECDH临时公钥,同时回复server_key_exchange,包含三部分重要内容:一是ECC相关的参数,二是ECDH临时公钥,三是ECC参数和公钥生成的签名值,用于客户端校验。
三、浏览器接收server_key_exchange 之后,使用证书公钥进行签名解密和校验,获取服务器端的ECDH临时公钥,生成会话所需要的共享密钥。
至此,浏览器端完成了密钥协商。
四、浏览器生成ECDH临时公钥和 client_key_exchange消息,跟RSA密钥协商不同的是,这个消息不需要加密了。
五、服务器处理client_key_exchang消息,获取客户端ECDH临时公钥。
六、服务器生成会话所需要的共享密钥,Server端密钥协商过程结束。
PS:密钥交换过程结束之后就得出了本次会话需要使用的对称密钥。
HTTPS使用成本
HTTPS目前唯一的问题就是它还没有得到大规模应用,受到的关注和研究都比较少。至于使用成本和额外开销,完全不用太过担心。一般来讲,使用 HTTPS 前大家可能会非常关注如下问题:
证书费用以及更新维护。大家觉得申请证书很麻烦,证书也很贵,可是证书其实一点都不贵,便宜的一年几十块钱,最多也就几百。而且现在也有了免费的证书机构,比如著名的 mozilla 发起的免费证书项目:let’s encrypt(https://letsencrypt.org/)就支持免费证书安装和自动更新。这个项目将于今年中旬投入正式使用。数字证书的费用其实也不高,对于中小网站可以使用便宜甚至免费的数字证书服务(可能存在安全隐患),像著名的 verisign 公司的证书一般也就几千到几万块一年不等。当然如果公司对证书的需求比较大,定制性要求高,可以建立自己的CA站点,比如google,能够随意签发google相关证书。
HTTPS降低用户访问速度。HTTPS对速度会有一定程度的降低,但是只要经过合理优化和部署,HTTPS对速度的影响完全可以接受。在很多场景下,HTTPS速度完全不逊于HTTP,如果使用SPDY,HTTPS的速度甚至还要比HTTP快。
HTTPS消耗CPU资源,需要增加大量机器。前面介绍过非对称密钥交换,这是消耗CPU计算资源的大户,此外,对称加解密,也需要CPU的计算。同样地,只要合理优化,HTTPS 的机器成本也不会明显增加。对于中小网站,完全不需要增加机器也能满足性能需求。